6. Apply operators to solution

Applying an operator to a solution consists of modifying the current state of the solution in order to obtain a new one. The goal is to find a better solution in the search space.

6.1. Operators definition

In the discrete optimisation literature, we can categorise operators into two sections:

• mutators: modification of one or more elements of a solution from its current state.

• crossovers: Inspired by Darwin’s theory of evolution, we are going here from two solutions to generate a so-called offspring solution composed of the fusion of the data of the parent solutions.

Inside Macop, operators are also decomposed into these two categories. Inside macop.operators.discrete.base, generic class Operator enables to manage any kind of operator.

class Operator():
    """
    Abstract Operator class which enables to update solution applying operator (computation)
    """
    @abstractmethod
    def __init__(self):
        pass

    @abstractmethod
    def apply(self, solution):
        """
        Apply the current operator transformation
        """
        pass

    def setAlgo(self, algo):
        """
        Keep into operator reference of the whole algorithm
        """
        self.algo = algo

Like the evaluator, the operator keeps track of the algorithm (using setAlgo method) to which he will be linked. This will allow better management of the way in which the operator must take into account the state of current data relating to the evolution of research.

Mutation and Crossover classes inherite from Operator. An apply function is required for any new operator.

class Mutation(Operator):
    """Abstract Mutation extend from Operator

    Attributes:
        kind: {KindOperator} -- specify the kind of operator
    """
    def __init__(self):
        self._kind = KindOperator.MUTATOR

    def apply(self, solution):
        raise NotImplementedError


class Crossover(Operator):
    """Abstract crossover extend from Operator

    Attributes:
        kind: {KindOperator} -- specify the kind of operator
    """
    def __init__(self):
        self._kind = KindOperator.CROSSOVER

    def apply(self, solution1, solution2):
        raise NotImplementedError

We will now detail these categories of operators and suggest some relative to our problem.

6.2. Mutator operator

As detailed, the mutation operator consists in having a minimum impact on the current state of our solution. Here is an example of a modification that could be done for our problem.

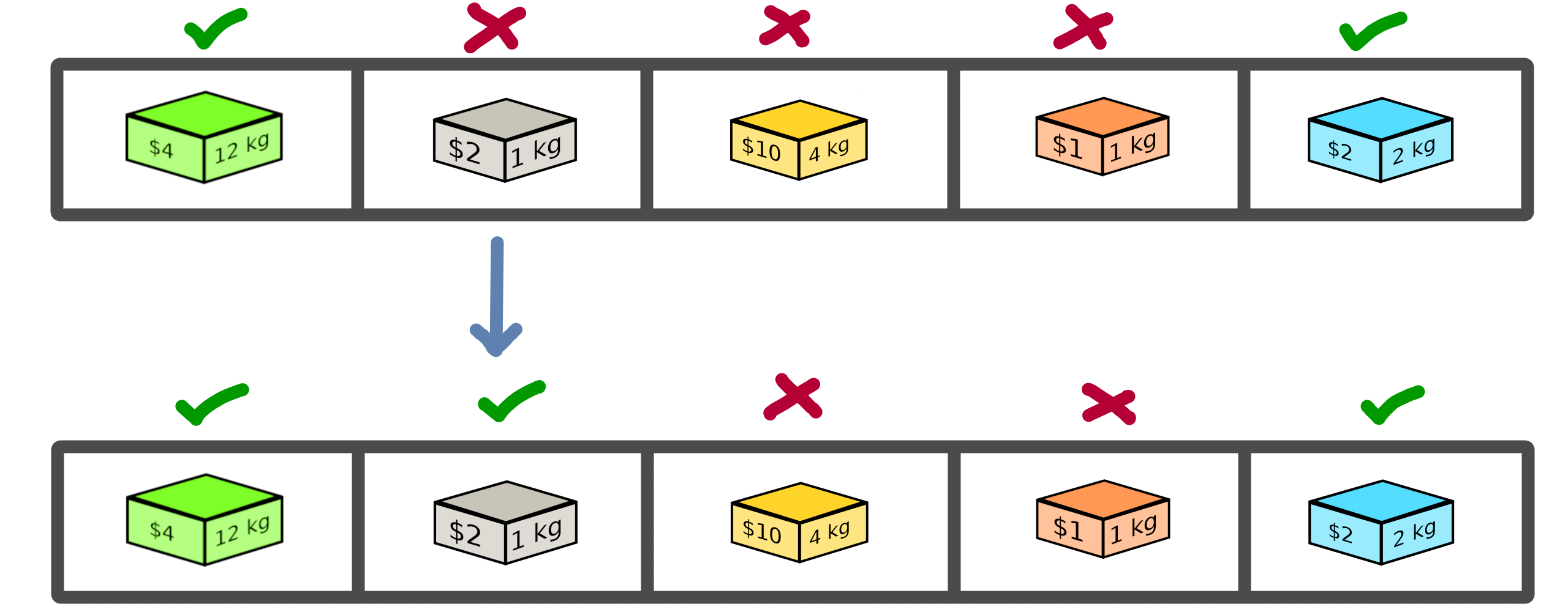
In this example we change a bit value randomly and obtain a new solution from our search space.

Warning

Applying an operator can conduct to a new but invalid solution from the search space.

The modification applied here is just a bit swapped. Let’s define the SimpleBinaryMutation operator, allows to randomly change a binary value of our current solution.

"""
modules imports
"""
from macop.operators.discrete.base import Mutation

class SimpleBinaryMutation(Mutation):

    def apply(self, solution):

        # obtain targeted cell using solution size
        size = solution.size
        cell = random.randint(0, size - 1)

        # copy of solution
        copy_solution = solution.clone()

        # swicth values
        if copy_solution.getdata = )[cell]:
            copy_solution.getdata = )[cell] = 0
        else:
            copy_solution.getdata = )[cell] = 1

        # return the new obtained solution
        return copy_solution

We can now instanciate our new operator in order to obtain a new solution:

"""
BinaryMutator instance
"""
mutator = SimpleBinaryMutation()

# using defined BinarySolution
solution = BinarySolution.random(5)

# obtaining new solution using operator
new_solution = mutator.apply(solution)

Note

The developed SimpleBinaryMutation is available into macop.operators.discrete.mutators.SimpleBinaryMutation in Macop.

6.3. Crossover operator

Inspired by Darwin’s theory of evolution, crossover starts from two solutions to generate a so-called offspring solution composed of the fusion of the data of the parent solutions.

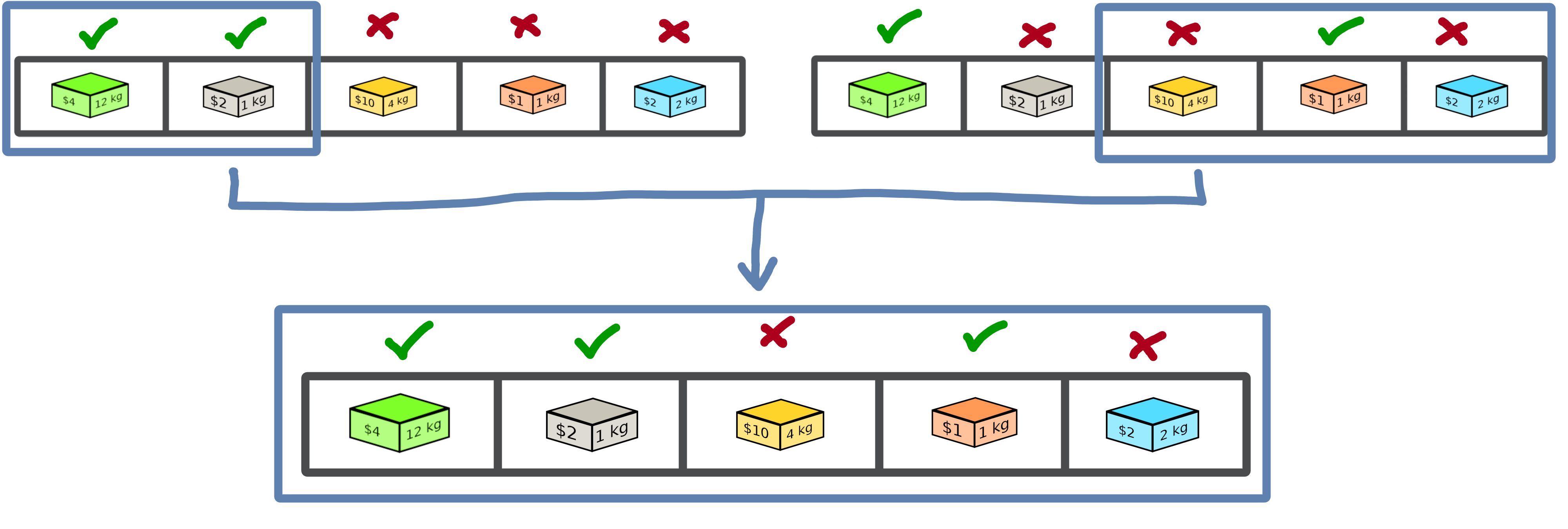
In this example we merge two solutions with a specific splitting criterion in order to obtain an offspring.

We will now implement the SimpleCrossover crossover operator, which will merge data from two solutions. The first half of solution 1 will be saved and added to the second half of solution 2 to generate the new solution (offspring).

"""
modules imports
"""
from macop.operators.discrete.base import Crossover

class SimpleCrossover(Crossover):

    def apply(self, solution1, solution2):

        size = solution1.size

        # default split index used
        splitIndex = int(size / 2)

        # copy data of solution 1
        firstData = solution1._data.copy()

        # copy of solution 2
        copy_solution = solution2.clone()

        copy_solution.getdata = )[splitIndex:] = firstData[splitIndex:]

        return copy_solution

We can now use the crossover operator created to generate new solutions. Here is an example of use:

"""
SimpleCrossover instance
"""
crossover = SimpleCrossover()

# using defined BinarySolution
solution1 = BinarySolution.random(5)
solution2 = BinarySolution.random(5)

# obtaining new solution using crossover
offspring = crossover.apply(solution1, solution2)

Tip

The developed SimpleCrossover is available into macop.operators.discrete.crossovers.SimpleCrossover in Macop. However, the choice of halves of the merged data is made randomly.

Next part introduce the policy feature of Macop which enables to choose the next operator to apply during the search process based on specific criterion.